Time Series

Paulo Fagandini

Nova SBE

Exercises

https://moodle.novasbe.pt/mod/folder/view.php?id=4021

Exercise 9.1

Let \(cGDP_t\) denote the annual percentage change in gross domestic product and let \(int_t\) denote a short-term interest rate. Suppose that \(cGDP_t\) is related to interest rate by

\[cGDP_t=\alpha_0+\delta_0 int_t + \delta_1 int_{t-1}+u_t\]

where \(u_t\) is uncorreltaed with \(int_t\), \(int_{t-1}\), and all other past values of interest rates. Suppose that the Federal Reserve follows the policy rule

\[int_t=\gamma_0 + \gamma_1 (cGDP_{t-1}-3)+v_t\]

where \(\gamma_1>0\). If \(v_t\) is uncorrelated with all past values of \(int_t\) and \(u_t\), argue that \(int_t\) must be correlated with \(u_{t-1}\). Which Gauss-Markov assumption does this violate?

\(cGDP_t=\alpha_0+\delta_0 int_t+\delta_1 int_{t-1}+u_t\) \(cGDP_{t-1}=\alpha_0+\delta_0 int_{t-1}+\delta_1 int_{t-2}+u_{t-1}\)

\(int_t=\gamma_0+\gamma_1(cGDP_{t-1}-3)+v_t\) \(int_t = \gamma_0 + \gamma_1(\alpha_0+\delta_0 int_{t-1}+\delta_1 int_{t-2}+u_{t-1}-3)+v_t\)

\(Cov(int_t, u_{t-1})=E[int_t u_{t-1}]=\) \(E[[ \gamma_0 + \gamma_1(\alpha_0+\delta_0 int_{t-1}+\delta_1 int_{t-2}+u_{t-1}-3)+v_t]u_{t-1}]\) \(E[\gamma_1 u_{t-1}^2]=\gamma_1 E[u_{t-1}^2]=\gamma_1 \sigma_u^2\)

This means that \(u_{t-1}\) and \(int_t\) are correlated, violating extrict exogeneity, and zero conditional mean, TS3.

Exercise 9.3

Using daily price and quantity observations on fish prices at Big Fish market in Lisbon we obtained the estimation results given below, where \(LAVGPRC\) is the logarithm of the average price of fish, \(MON\), \(TUES\), \(WED\), and \(THURS\) are daily dummy variables, and \(T\) is a linear time trend.

Exercise 9.3

Exercise 9.3

1. Interpret the coefficient estimate on the linear time trend.
2. Is there evidence that prices vary systematically within a week? How would you formally test for this hypothesis?

a \(\hat{\beta}_t=-0.00399\): the average daily percentage change in the fish price after accounting for seasonal effects is equal to -0.3991%.

b No, because the daily dummy variables are not statistically significant (the p-values associated with the four daily dummy variables are greater than 10%).

To formally test for the presence of seasonality,w e need to perform a jount significance test of the four daily dummy variables:

\(H_0: \beta_{mon}=\beta_{tue}=...=0\), \(H_a: Not\) \(F=\frac{\frac{R_u^2-R_R^2}{4}}{\frac{1-R_u^2}{97-5-1}}\sim F(4,91)\)

If \(F>F^c\) we reject the null hypothesis. The restricted model is \(lavgprc=\beta_0+\beta_1 t + u_t\).

Exercise 9.3

Now consider the table below here we include two new variables \(WAVE2\) and \(WAVE3\), which are measures of wave heights over the past few days.

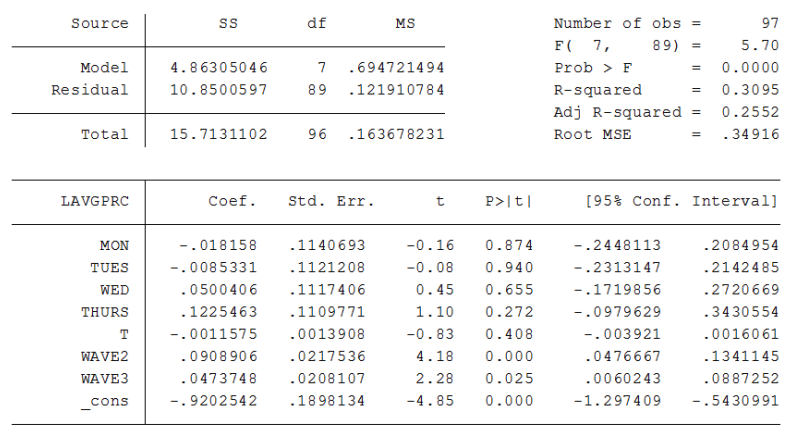
Exercise 9.3

3. Are these variables individually significant? Describe an economic mechanism by which story seas woudl increase the price of fish.

4. What happened to the time trend when the two new variables were included in the regression? What must be going on?

5. Why do you expect all thej explanatory variables to be strictly exogenous? Explain briefly the difference between conteporaneus exogeneity and strict exogeneity.

c \(WAVE2\) and \(WAVE3\) are individually statistically significant at 5% level, because their associated p-values are below 5%. Stormy seas lead to less supply of fish and tehrefore for the same demand the price of fish would increase.

d In the extended model \(\hat{\beta}_t=-0.0011575\) and the corresponding p-value is greater than 5% and therefore the time trend is not statistically significant in this model. In the initial model \(\hat{\beta}_t=-0.003991\) and the associated p-value is lower than 5%, i.e., it is individuall statistically significant.

From the omitted variable bias expression we know that \(-0.003991 = -0.00011575+bias\). Then, the bias is negative. This means that the height of the waves must be correlated with the time trend.

e The time trend and the daily dummy variables are strictly exogenous because they are just functions of time and the calendar. Furthermore, the height of waves is not influenced by past, present or future unexpected changes in the (log) average price of fish.

Contemporaneous exogeneity \(E[u_t|x_t]=0\): the error term and the set of explanatory variables are contemporaneously uncorrelated. Strict exogeneity: \(E[u_t|x_t]=0\) the error term at time \(t\) is uncorrelated with each explanatory variable at every time period (past or future).

Exercise 10.2

Let \(e_t\) be a sequence of independent identically distributed rvs with mean 0 and variance 1. Define a stochastic process by:

\[ x_t=e_T-0.5 e_{t-1}+0.5 e_{t-2}\]

for \(t=1,2,...\)

1. Find \(E[x_t]\) and \(V[x_t]\). Do either of these depend on \(t\)?
2. Show that \(Corr(x_t,x_{t+1})=-0.5\) and \(Corr(x_t,x_{t+2})=1/3\)

a \(E[x_t]=E[e_t-0.5 e_{t-1}+0.5 e_{t-2}]=E[e_t]-0.5 E[e_{t-1}]+0.5 E[e_{t-2}]=0\) \(V[x_t]=V[e_t-0.5 e_{t-1}+0.5 e_{t-2}]=V[e_t]+0.25 V[e_{t-1}]+0.25 V[e_{t-2}]=3/2\)

b \(Cov(x_t,x_{t+1})=E[x_t x_{t+1}]=E\left[(e_t+0.5 e_{t-1}-0.5 e_{t-2})(e_{t+1}+0.5 e_{t}-0.5 e_{t-1})\right]\) \(=-0.5 E[e_t^2]+0.5^2 E[e_{t-1}^2]=0.5 V[e_t]-0.5^2 V[e_{t-1}]=-3/4\) \(Corr(x_t,x_{t+1})=\frac{Cov(x_t,x_{t+1})}{V[x_t]}=-\frac{3/4}{3/2}=-\frac{1}{2}\) \(Cov(x_t,x_{t+2})=E[x_t,x_{t+2}]=E[(e_t-0.5e_{t-1}+0.5e_{t-2})(e_{t+2}-0.5e_{t+1}+0.5 e_t)]\) \(=0.5 E[e_t^2]=\frac{1}{2}\)

\(Corr(x_t,x_{t+2})=\frac{Cov(x_t,x_{t+2})}{V{x_t}}=\frac{1/2}{3/2}=\frac{1}{3}\)

Exercise 10.2

3. What is \(Corr(x_t,x_{t+h})\) for \(h>2\)>
4. Is \(x_t\) an asymptotically uncorrelated process?

c \(Cov(x_t,x_{t+3})=E[x_t,x_{t+3}]=E[(\dots)(\dots)]=0\) because \(x_t\) only depends on \(e_{t+j}\) \(j\leq 0\), and \(x_{t+j}\) only depends on \(e_{t+j}\) \(j>0\). Then \(Corr(x_t,x_{t+h})=0\) \(\forall h>2\), because \(e_t\) is iid with zero mean and \(E[e_t,e_s]=0\) \(\forall t\neq s\).

d Asymptotically uncorrelated process: a covariance stationary process where \(Cov(x_t,x_{t+h})\rightarrow 0\) as \(h\rightarrow\infty\) Yes, because terms more than two periods apart are actually uncorrelated, and so it is clear thant \(Corr(x_t,x_{t+h})\rightarrow 0\) as \(h\rightarrow\infty\).